最大网络流 |
您所在的位置：网站首页 › min max算法 › 最大网络流 |
最大网络流
|
问题描述在图 G(V,E) 中，每条边 (u,v) 有容量 c(u,v)\geq{0} ，可定义每条边的实际流量为 f(u,v) 初始时所有传输量都在源点 s ，需要找出如何最快的把所有传输量转移到汇点 t 的可行流的，有以下三个限制三大限制容量限制： f(u,v)\leq{c(u,v)} 反对称性： f(u,v)=-f(v,u) 流量平衡：除源点和汇点外，其余任意结点流入流量和等于流出流量和，即对任意结点v， \sum_{u\in{V}}f(v,u)=0 总之，最大流问题，就是求解流量 F=\sum_{v\in{V}}f(s,v) 最大，接下来将以标号法作为引入（例题分析+原理解释），再使用 Edmond-Karp、Dinic、ISAP、HLPP 算法（含详细代码）进行求解。 核心概念零流弧： f(u,v)=0 的边 饱和弧： f(u,v)0，则给顶点 v_j 标号 (v_i, \delta_j), \delta_j=min\{\delta_i,f_{ji}\} 当无法选择后，若终点 v_i 得到标号，说明存在增广链，转到调整阶段，否则说明不存在增广链，此时可行流 f 即为最大流调整过程应用反向追踪法，从终点 v_t 及其其他顶点的第一个标号，找出增广链如： v_s 第一标号为 v_k ，则 (v_k, v_s) 是增广路上的边，此时可把 v_k 看做子链中的 v_s ，继续向下搜索，直到找到 v_t ，将选择到的边连成增广路。找到增广路后，修改流 f'=\begin{cases} f_{ij}+\delta_i,(v_i,v_j)\in{u^+} \\ f_{ij}-\delta_i,(v_i,v_j)\in{u^-} \\ f_{ij},(v_i,v_j)\not\in{u} \end{cases}调整结束后去掉所有标号，再次进行标号过程。样例一 反向边是整个最大流算法中最巧妙的部分，本质上就是利用了抵消的原理，如下图 留下一个标记，让后面的流有机会让前面的流走另一条路。假设一次搜索到的增广路为 S\rightarrow{3}\rightarrow{5}\rightarrow{t} ，并更新残量网后得到下图  下一次对 5 的邻接点进行增广，发现 5\rightarrow{3} 有一条反向边容量为 10，这时候当我们利用了这条边，就可以和我们之前利用其对应的正向边相互作用抵消，将容量还原给正向边  代码实现以洛谷模版题为例：P3376 【模板】网络最大流 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)代码：AC代码（邻接矩阵数据结构存储）注：题目使用代码中使用 Long 类型、并对原代码适应的样例的输入格式。// 核心部分代码（可对 GPoint、GEdge 等进行进一步封装优化，由于代码过长这里进行了简化）
// 本代码输出每次增广的情况，常用于进行小规模的数据测试
public class GraphUtils {
/**
* edmondsKarp 算法主函数
* @param sourceNum
* @param targetNum
* @param edges
* @param n
* @return
*/
private static double edmondsKarp(int sourceNum, int targetNum, double[][] edges, int n) {
double maxFlow = 0D;
int[] preNum = new int[n + 10];
while (true) {
// 找增广路（标号过程）
double nowFlow = bfsEK(sourceNum, targetNum, edges, preNum, n);
if (nowFlow == -1) {
break;
}
// 调整过程
int cur = targetNum;
StringBuilder road = new StringBuilder();
road.append(cur);
while (cur != sourceNum) {
int fa = preNum[cur];
edges[cur][fa] += nowFlow;
edges[fa][cur] -= nowFlow;
cur = fa;
road.insert(0, cur + " -> ");
}
System.out.println("this road : " + road + ", addFlow : " + nowFlow);
maxFlow += nowFlow;
}
System.out.println("End Graph Struct");
System.out.println(maxFlow);
return maxFlow;
}
/**
* 广搜 增广路径
* @param sourceNum 源点
* @param targetNum 汇点
* @param edges 邻接矩阵
* @param n 顶点数
* @return
*/
private static double bfsEK(int sourceNum, int targetNum, double[][] edges, int[] preNum, int n) {
Arrays.fill(preNum, -1);
double[] flow = new double[n + 10];
flow[sourceNum] = Double.MAX_VALUE;
preNum[sourceNum] = 0;
ArrayDeque arrayDeque = new ArrayDeque();
arrayDeque.add(sourceNum);
while (!arrayDeque.isEmpty()) {
int u = arrayDeque.pop();
if (u == targetNum) {
break;
}
for (int i = 0; i |
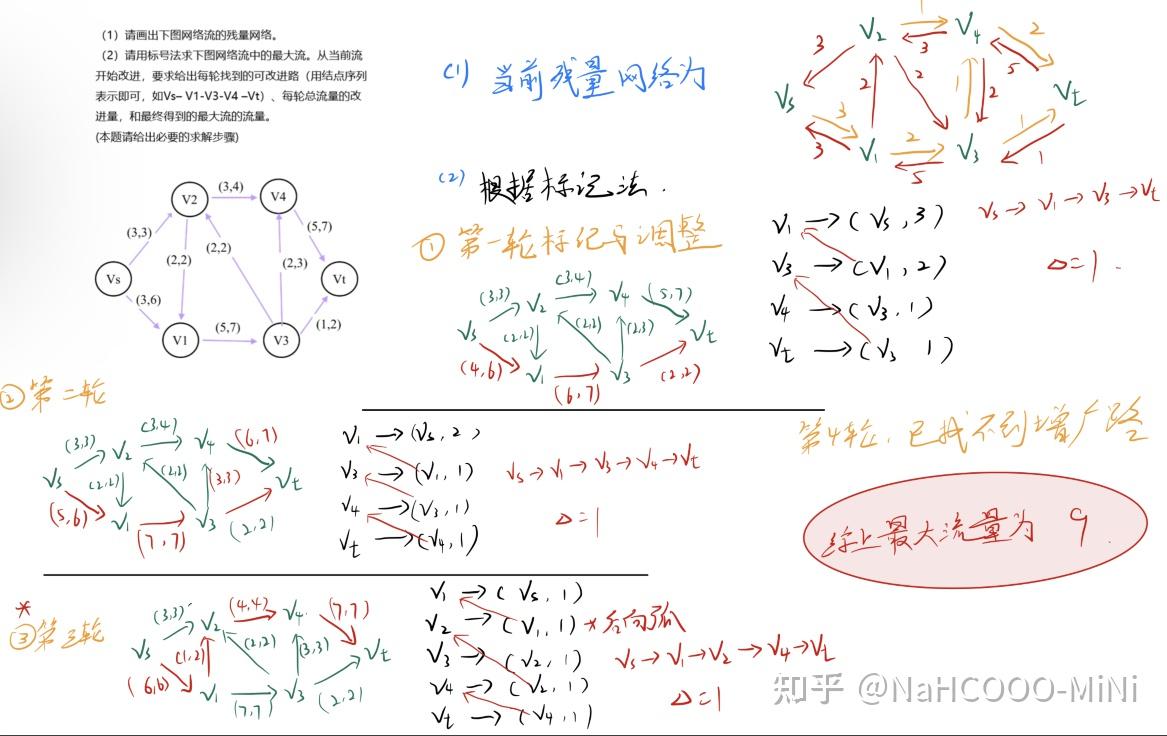样例二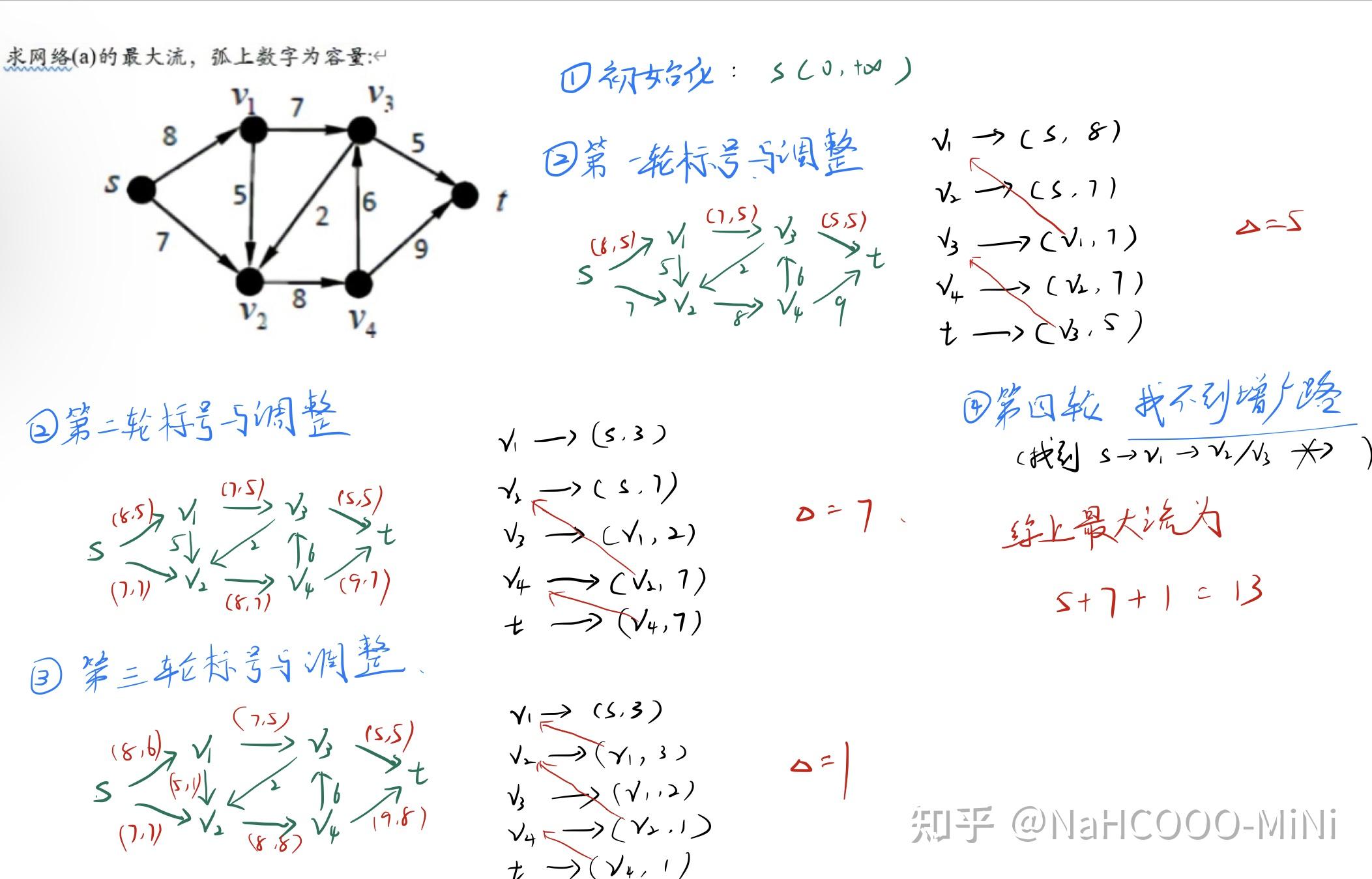
Ford-Fullerson 方法核心：根据标号法中的思想优化搜索增广路和调整。需要通过反向边的测回机制，来保证当找不到增广路时，流到汇点的浏览就是最大流。注：Fork-Fullerson 方法是后续几种算法实现的基础。基本搜索思路初始所有边的流量为 0找到一条增广路更新残留网络不断重复 2、3 操作，直到找不到增广路Edmond-Karp 算法本质上是 Ford-Fullerson 的 BFS 写法，避免了使用 DFS 搜索中可能会 "绕远路" 的问题，可以保证每次找到的都是最短的增广路，复杂度上限是 O(ve^2) 反向边理解【本文地址】
今日新闻 |
推荐新闻 |